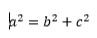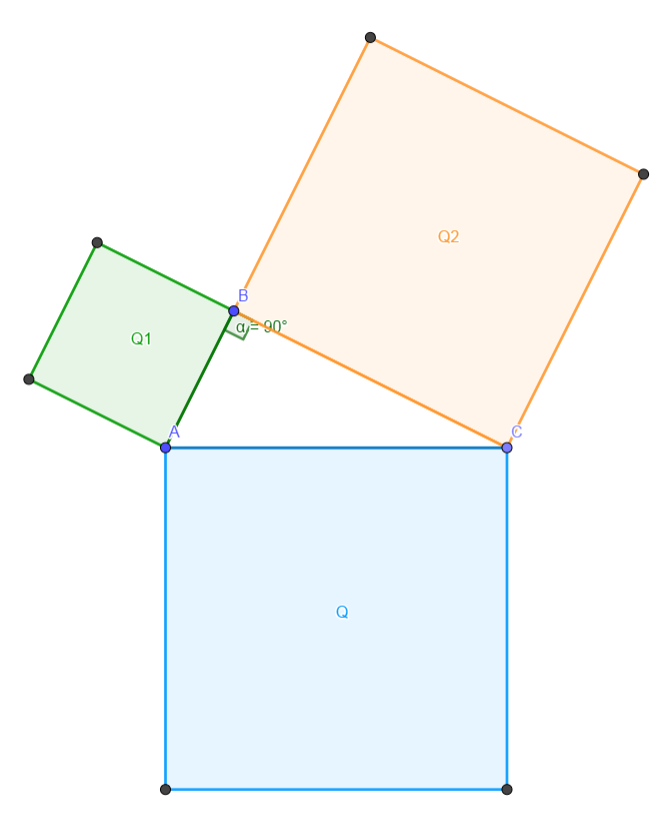
TEOREMA: ” In ogni triangolo rettangolo, il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti. “
DIMOSTRAZIONE:

Tracciamo l’altezza BH e prolunghiamola in modo da scomporre il quadrato Q nei rettangoli R1 e R2:
Q = R1 + R2
L’altezza Bh individua sull’ipotenusa i segmenti AH e CH, proiezioni dei cateti. Inoltre AH e CH sono le basi di R1 e R2, che hanno i lati congruenti alla proiezione di un cateto e all’ipotenusa. Quindi, per il primo teorema di Euclide, abbiamo:
Q1 = R1, Q2 = R2
Poiché somme di figure equivalenti sono equivalenti, risulta:
R1 + R2 = Q1 + Q2
Essendo Q = R1 + R2 e R1 + R2 = Q1 + Q2, per la proprietà transitiva dell’equivalenza si ottiene:
Q = Q1 + Q2.
Vale anche il teorema inverso.
Passando alle misure, indicando con a,b,c rispettivamente le misure dell’ipotenusa e dei cateti del triangolo rettangolo ABC, possiamo scrivere: