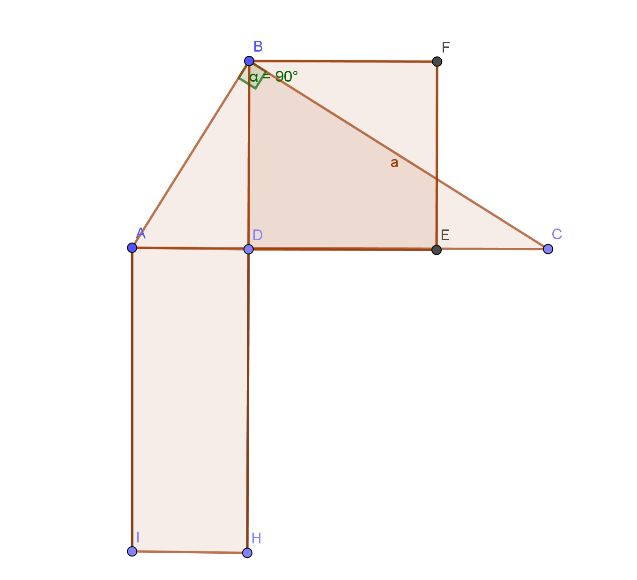
TEOREMA: In ogni triangolo rettangolo il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo avente i lati congruenti alle proiezioni dei cateti sull’ipotenusa.
DIMOSTRAZIONE:
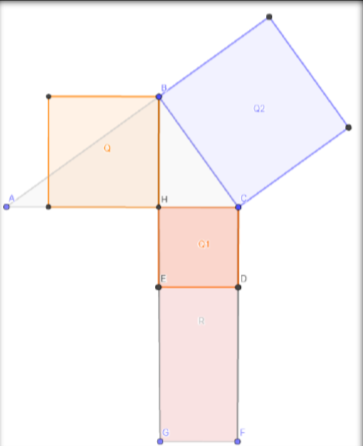
Tracciamo BH, altezza relativa all’ipotenusa AC.
Disegniamo: il quadrato Q2 di lato BC, il quadrato Q di lato BH; il rettangolo R1 di base CH e altezza CF = Ac, ossia il rettangolo CFGH.
Consideriamo su CF il punto D tale che CD = CH e su HG il punto E tale che HE = CH. Chiamiamo Q1 il quadrato CDEH. Poiché CF = AC e CD = CH, il rettangolo EDFG è R.
Il rettangolo R1 è formato dal quadrato Q1 e dal rettangolo R. Vale cioè la seguente relazione:
R1 = Q1 + R
Applicando al triangolo HBC il teorema di Pitagora otteniamo:
Q2 = Q + Q1
Q = Q2 – Q1
Applichiamo al triangolo ABC il primo teorema di Euclide:
Q2 = R1 quindi Q2 = R + Q1 quindi R = Q2 – Q1.
Essendo Q e R equivalenti entrambi a Q2 – Q1, sono equivalenti fra loro per la proprietà transitiva:
Q = R.
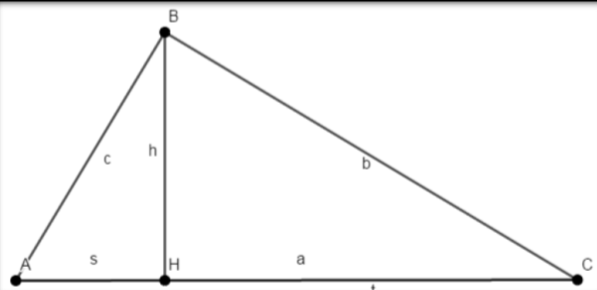
Passando alle misure, consideriamo il triangolo ABC e indichiamo con:
- a,b,c rispettivamente le misure dell’ipotenusa e dei cateti;
- h la misura dell’altezza BH relativa all’ipotenusa;
- s,t rispettivamente le misure delle proiezioni AH e HC dei cateti sull’ipotenusa.
Applicando il secondo teorema di Euclide otteniamo :
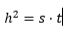
da cui si ricava:
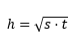
DA UN RETTANGOLO A UN QUADRATO EQUIVALENTE
Una delle possibili applicazioni dei teoremi appena visti è la costruzione di figure equivalenti a partire da una figura data.
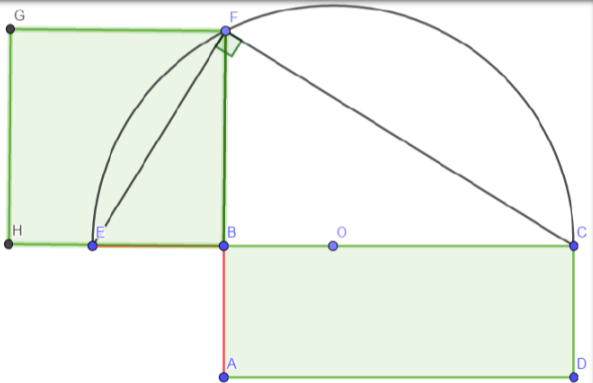
Vediamo in che modo è possibile costruire un quadrato equivalente a un rettangolo dato.
Disegniamo un rettangolo ABCD qualsiasi. Prolunghiamo un suo lato maggiore, per esempio BC, dalla parte di B, di un segmento BE congruente al lato minore AB: BE = AB.
Troviamo il punto medio O di EC, e disegniamo la semicirconferenza di centro O e raggio OC, dalla parte in cui non interseca il rettangolo.
Prolunghiamo AB fino a incontrare la semicirconferenza nel punto F. Congiungiamo F con E e con C. Il triangolo EFC è rettangolo perché inscritto in una semicirconferenza.
BE e BC sono le proiezioni sull’ipotenusa dei cateti FE e FC e sono congruenti ai lati del rettangolo.