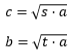TEOREMA: “In ogni triangolo rettangolo, il quadrato costruito su un cateto è equivalente al rettangolo che ha i lati congruenti all’ipotenusa e alla proiezione dello stesso cateto sull’ipotenusa.”
DIMOSTRAZIONE:
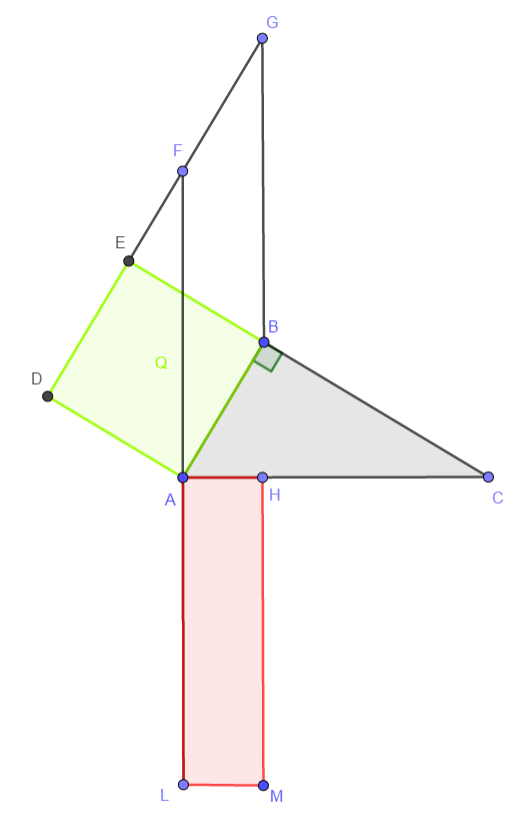
I triangoli ABC e AFD hanno:
- AB=AD, per costruzione (ADEB è un quadrato);
- angolo B= angolo D, retti per costruzione;
- α = γ perché complementari dello stesso angolo β.
Pertanto sono congruenti per il secondo criterio. Im particolare hanno AC = AF.
Il quadrilatero AFGB è un parallelogramma, perché ha i lati opposti paralleli per costruzione.
Il parallelogramma AFGB e il quadrato ADEB hanno la stessa base AB e la stessa altezza AD, quindi sono equivalenti.
Il parallelogramma AFGB e il rettangolo ALMH hanno basi congruenti AF = AL (perché entrambe congruenti all’ipotenusa) e la stessa altezza AH, quindi sono equivalenti.
Poiché ADEB = AFGB e AFGB = ALMH, per la proprietà transitiva dell’equivalenza abbiamo anche ADEB = ALMH, ossia Q = R.
In modo del tutto analogo, si può procedere eseguendo la costruzione sull’altro cateto.
Passando alle misure è possibile, utilizzando l’equivalenza trovata, determinare l’uguaglianza fra le misure delle aree delle figure
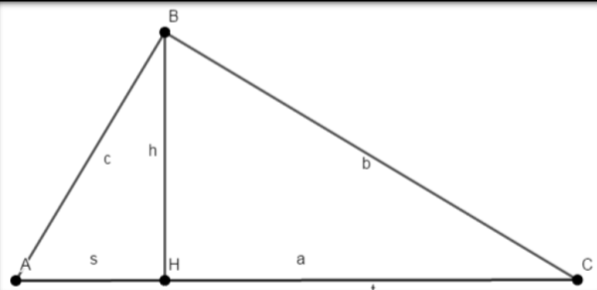
Nel triangolo ABC indichiamo con:
- a,b,c rispettivamente le misure dell’ipotenusa e dei cateti BC e AB;
- h la misura dell’altezza BH relativa all’ipotenusa;
- s, t rispettivamente le misure delle proiezioni AH e HC dei cateti sull’ipotenusa.
Applicando il primo teorema di Euclide otteniamo:
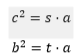
Le relazioni permettono di calcolare le misure dei cateti, note le misure dell’ipotenusa e delle proiezioni dei cateti sull’ipotenusa stessa :