PRIMO TEOREMA DI EUCLIDE:
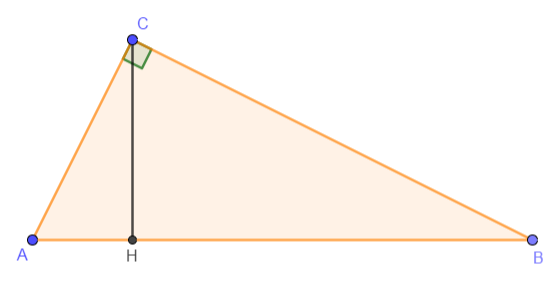
Calcoliamo il perimetro di un triangolo rettangolo le cui proiezioni dei cateti sull’ipotenusa sono lunghe 13 cm e 36 cm.
SOLUZIONE:
La misura dell’ipotenusa è AB= 13 + 36 = 49 cm.
Applichiamo il primo teorema di Euclide per trovare AC :
AC ² = AB · AH quindi AC ² = 49 · 13.
Estraiamo la radice quadrata:
AC= √ 49 · 13 = 7 √ 13 cm
Applichiamo ancora il primo teorema di Euclide per trovare BC:
BC ² = AB · BH quindi BC = √ 49 · 36 = 42 cm
La lunghezza del perimetro del triangolo espressa in cm è :
49 cm + 42 cm + 7 √ 13 cm = ( 91 + 7 √ 13 ) cm.
TEOREMA DI PITAGORA :
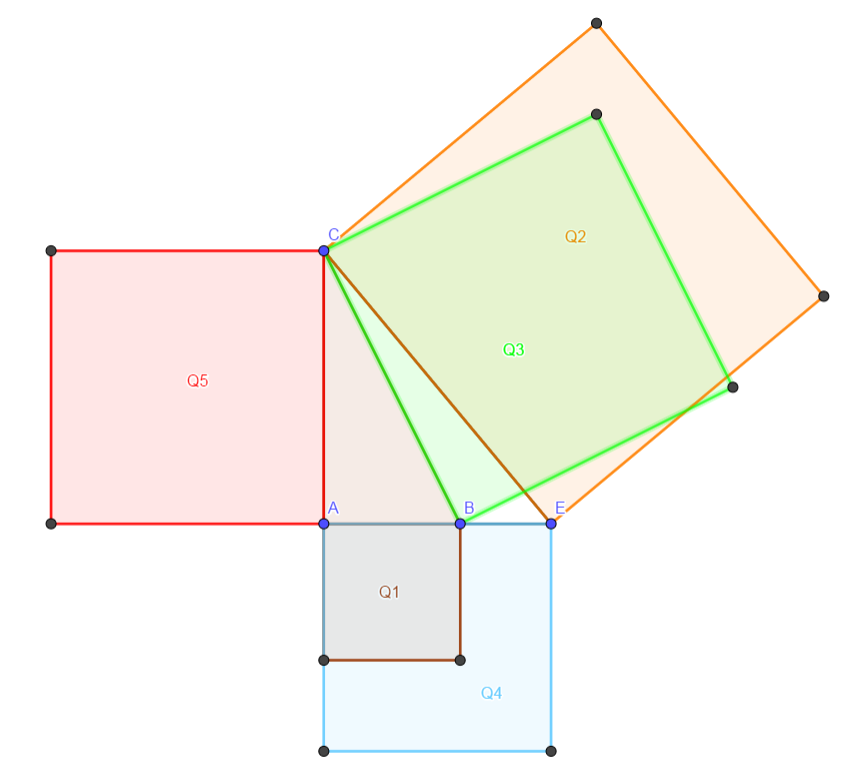
in un triangolo rettangolo ABC prolunghiamo il cateto AB di un segmento a piacere BE. Dimostriamo che la somma dei quadrati costruiti sui segmenti AB e CE è equivalente alla somma dei quadrati costruiti su BC e AC.
SOLUZIONE:
Applichiamo il teorema di Pitagora ai triangoli rettangoli AEC e ABC. Otteniamo:
Q2 = Q4 + Q5 e Q3 = Q1 + Q5
Per la proprietà simmetrica dell’equivalenza possiamo scrivere Q1 + Q5 = Q3. Sommando membro a membro questa equivalenza con Q2 = Q4 + Q5, otteniamo :
Q1 + Q5 + Q2 = Q3 + Q4 + Q5.
Sottraendo dai due membri dell’equivalenza il termine Q5, otteniamo infine:
Q1 + Q2 = Q3 + Q4.
APPLICAZIONI DEL TEOREMA DI PITAGORA:
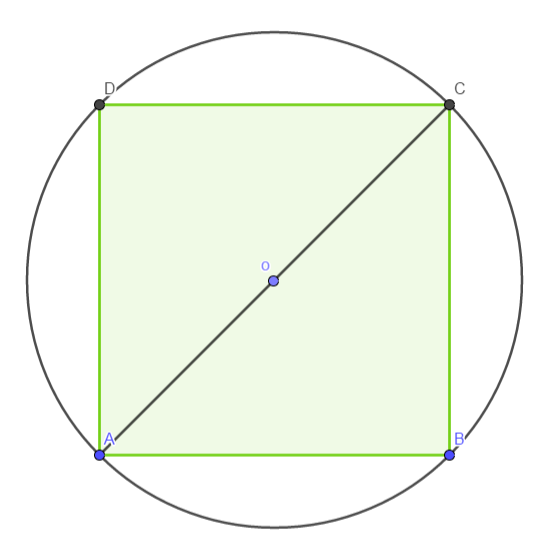
Conoscendo il segmento AO in figura che misura 5 √ 2 cm, calcoliamo l’area del segmento circolare individuato da DC.
SOLUZIONE:
Il quadrato ABCD è inscritto in una circonferenza di diametro AC. Ricordando che fra le misure d e l della diagonale e del lato di un quadrato esiste la relazione d = l √ 2, possiamo scrivere:
AC = AB √ 2.
La diagonale coincide con il diametro della circonferenza, perciò:
AC = 2 x 5 √ 2 = 10 √ 2 ; 10 √ 2 = AB x √ 2 quindi AB = 10.
La misura dell’area del quadrato è : Aq= 100.
La misura dell’area del cerchio è : Ac= π ( 5 √ 2) ² = 50 π
L’area del segmento circolare è la quarta parte della differenza fra l’area del cerchio e l’area del quadrato:
A = ( 50 π – 100) : 4 = 25 ( π /2 -1) cm.
SECONDO TEOREMA DI EUCLIDE:
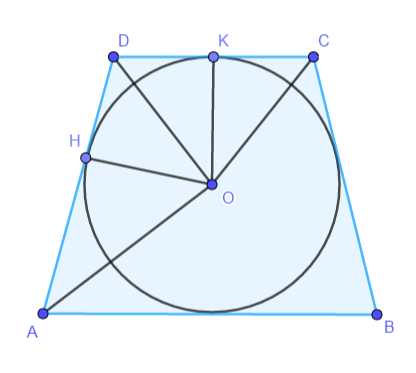
Dimostriamo che, in un trapezio isoscele circoscritto a una circonferenza, il quadrato del raggio è equivalente al rettangolo che ha per dimensioni le semibasi del trapezio.
SOLUZIONE:
nel triangolo DOA, l’angolo ADO= 1/2 ADC e l’angolo DAO= 1/2 DAB per il teorema delle tangenti da un punto esterno a una circonferenza.
Poiché CDA + DAB = π , essendo angoli coniugati interni delle rette parallele AB e DC con trasversale DA, ne segue che ADO + DAO = π /2, perciò il triangolo DOA è rettangolo in O.
Tracciamo OH = r nel punto di tangenza ( OH ⊥ DA).
Applichiamo il secondo teorema di Euclide al triangolo DOA: Q( OH) = R (DH;HA ).
Tracciamo OK ⊥ CD e consideriamo i triangoli rettangoli DHO, DKO, KOC:
- OH = OK perché raggi della circonferenza;
- HDO = ODK = KCO perché metà di angoli congruenti.
Oerciò i triangoli DHO, DKO, KOC sono congruenti per il secondo criterio di congruenza dei triangoli rettangoli, in particolare:
DH = DK = KC, ossia DH = 1/2 CD.
Analogamente si dimostra che HA = 1/2 AB.
Sostituiamo nell’equivalenza precedente e otteniamo : Q (r) = R ( AB/2; CD/2).