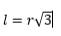Il teorema di Pitagora viene utilizzato per risolvere molti problemi di geometria con figure nelle quali sono presenti triangoli rettangoli. Ne vediamo alcuni.
LA DIAGONALE DEL QUADRATO
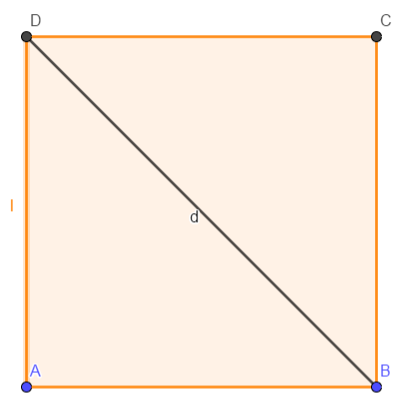
La misura della diagonale del quadrato è uguale al prodotto della misura del suo lato per la radice quadrata di 2.
Consideriamo un quadrato il cui lato misura l e indichiamo con d la misura della sua diagonale.
La diagonale divide il quadrato in due triangoli rettangoli che hanno per cateti il lato l del quadrato e per ipotenusa la diagonale d.
Applicando il teorema di Pitagora a uno di questi triangoli rettangoli, per esempio ABD, otteniamo:
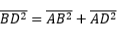
da cui :
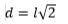
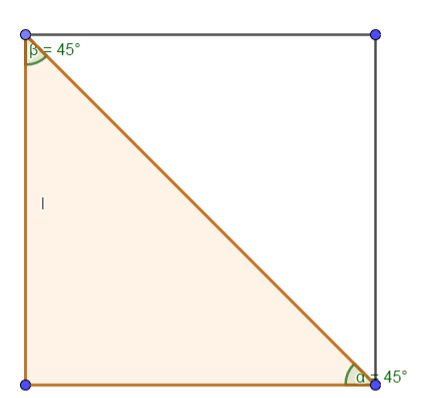
Consideriamo ora un triangolo rettangolo isoscele ABC. I suoi due cateti sono congruenti e gli angoli misurano 45°. Un triangolo con queste caratteristiche è la metà di un quadrato che ha per lato un cateto e per ipotenusa la diagonale.
Pertanto la misura di d dell’ipotenusa del triangolo rettangolo si ottiene moltiplicando per la radice quadrata di 2 la misura del cateto.
L’ALTEZZA DEL TRIANGOLO EQUILATERO
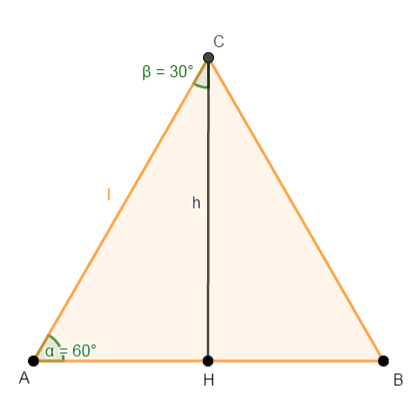
In un triangolo equilatero la misura dell’altezza è uguale al prodotto della misura della metà del suo lato per la radice quadrata di 3.
Consideriamo un triangolo equilatero ABC, di cui conosciamo la misura l del lato. Tracciamo l’altezza CH relativa al lato AB e indichiamo con h la sua misura. Il triangolo ABC rimane diviso in due triangoli rettangoli, perciò possiamo applicare il teorema di Pitagora, per esempio al triangolo CAH. L’altezza è anche mediana, perciò : AH = HB = l/2.
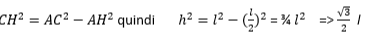
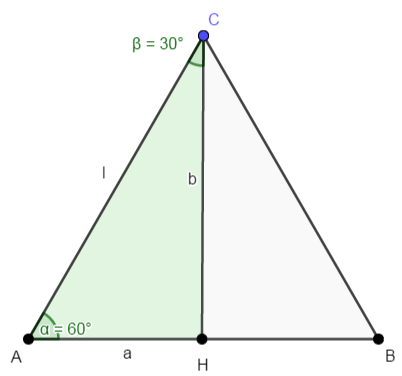
Consideriamo ora un triangolo rettangolo con gli angoli acuti rispettivamente di 30° e 60°. Esso è uguale alla metà di un triangolo equilatero, che ha l’ipotenusa congruente a un lato. Indicando con l la misura dell’ipotenusa, ricaviamo le misure dei cateti a e b utilizzando le relazioni trovate per il triangolo equilatero.
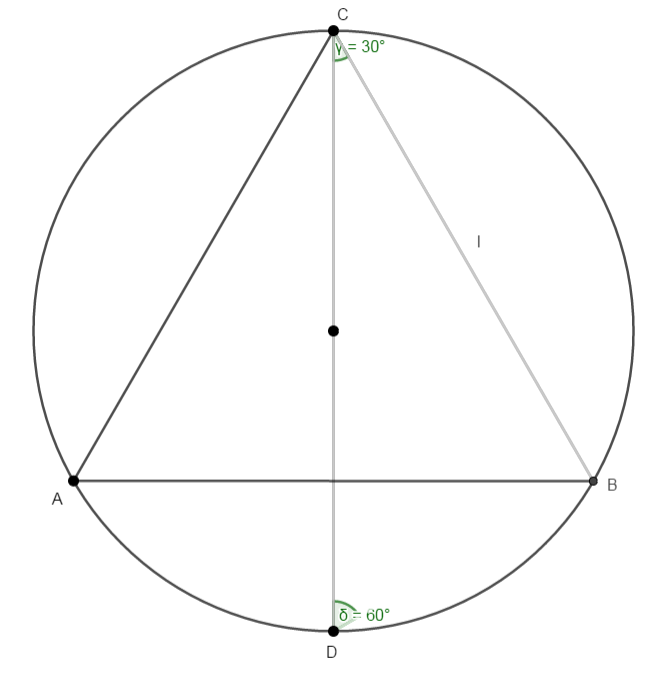
In ogni triangolo equilatero inscritto in una circonferenza di raggio r la misura del lato è uguale al prodotto del raggio per la radice quadrata di 3.
Consideriamo un triangolo equilatero ABC, di lato l, inscritto in una circonferenza di raggio r.
Prolunghiamo l’altezza CH fino a incontrare la circonferenza nel punto D. Il triangolo CBD è un triangolo rettangolo, perchè inscritto in una semicirconferenza; l’angolo BCD è di 30°, perciò l’angolo CBD è di 60 °, quindi DB = 1/2 CD = r.
Applicando il teorema si Pitagora al triangolo CBD otteniamo: